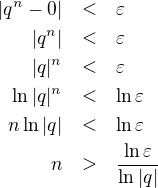Limita geometrické posloupnosti

Z MatWiki

Zadání

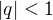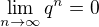Dokažte, že pro $LaTeX: |q|<1$ platí: $LaTeX: \lim_{n\rightarrow\infty}q^n=0$ .

Řešení

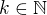Podle definice musíme ukázat, že pro libovolné kladné $LaTeX: \varepsilon$ je od určitého $LaTeX: k\in\mathbb N$ nerovnice

$LaTeX: |q^n-0|<\varepsilon$

splněná pro všechna 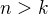$LaTeX: n>k$ . Nerovnici budeme postupně upravovat:

$LaTeX: \parstyle\begin{eqnarray*}|q^n-0|&<&\varepsilon\\ |q^n|&<&\varepsilon\\|q|^n&<&\varepsilon\\\ln|q|^n&<&\ln\varepsilon\\n\ln|q|&<&\ln\varepsilon\\n&>&\frac{\ln\varepsilon}{\ln|q|} \end{eqnarray*}$

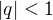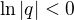Poznámka: protože je $LaTeX: |q|<1$ , je $LaTeX: \ln|q|<0$ . Na posledním řádku jsme nerovnici dělili záporným číslem, a proto se změnil znak nerovnosti.\\

Výraz 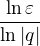$LaTeX: \frac{\ln\varepsilon}{\ln|q|}$ je jednoznačně definovaný a pro zadané 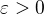$LaTeX: \varepsilon>0$ ho lze vždy vypočítat. Stačí tedy vzít za 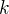$LaTeX: k$ první celé číslo větší než 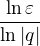$LaTeX: \frac{\ln\varepsilon}{\ln|q|}$ a nerovnice 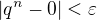$LaTeX: |q^n-0|<\varepsilon$ bude vždy platit. QED

Limita geometrické posloupnosti

Z MatWiki

Zadání

Řešení

Zobrazení

Osobní nástroje

Navigace

Hledat

Nástroje