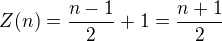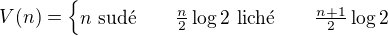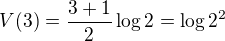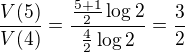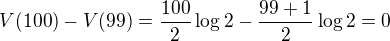Příklad 11
Z MatWiki
Zadání
Pro 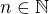 je definován výraz:
je definován výraz:
- Vyjádřete jediným členem
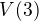 .
.
- Vypočítejte podíl
 .
.
- Vypočítejte rozdíl
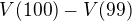 .
.
Řešení
Podle pravidel pro počítání s logaritmy můžeme 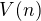 přepsat do tvaru
přepsat do tvaru
Nyní se budeme zabývat pouze výrazem v závorce (označíme 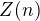 ) a rozbor rozdělíme na dva případy:
) a rozbor rozdělíme na dva případy:
(a) 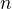 je sudé. Pak můžeme sečíst sousední dvojice
je sudé. Pak můžeme sečíst sousední dvojice
Protože dvojic je 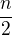 a každá přispívá do součtu jedničkou, je výsledný součet
a každá přispívá do součtu jedničkou, je výsledný součet
(b) 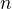 je liché. Nyní bude součet
je liché. Nyní bude součet
Dvojic je 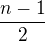 a ještě jedna jednička navíc
a ještě jedna jednička navíc
Dostáváme tak vztah pro 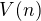
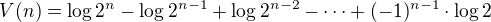
![LaTeX: V(n)=\log2[n-(n-1)+(n-2)-\cdots+(-1)^{n-1}]](/math/a6d1e4f2a18b557e5043a52486878cb2.gif)
![LaTeX: Z(n)=\underbrace{n-(n-1)}_1+\underbrace{(n-2)-(n-3)}_1+\dots+\underbrace{[n-(n-2)]-[n-(n-1)]}_1](/math/0461c0c72f5b059768f44ef59d4c9d26.gif)
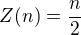
![LaTeX: Z(n)=\underbrace{n-(n-1)}_1+\underbrace{(n-2)-(n-3)}_1+\dots+\underbrace{[n-(n-3)]-[n-(n-2)]}_1+\underbrace{[n-(n-1)]}_1](/math/51d5335db80f0664cf8547f2930bc2b9.gif)