Počty relací na konečné množině

Z MatWiki

Symetrické relace

Pojem relace je velmi základním pojmem v celé matematice a jeho pochopení je tedy velmi důležité. Nejdřív je dobré si uvědomit, co to relace je. Je to LIBOVOLNÁ podnožina kartézského součinu dvou (ne nutně různých) množin. To znamená, že relace nad množinou X je prostě nějaká podmnožina množiny uspořádaných dvojic (a, b), kde a i b patří do množiny X.

Relaci si mohu představit jako jakousi tabulku, kde prázné políčko znamená, že dva prvky nejsou v relaci a plné že naopak v relaci jou. Mějme třeba takovouto relaci na množině {1, 2, 3, 4, 5}. Řádky představují první prvek dvojice (a, b) a sloupce druhý.

   1  2  3  4  5
1 X
2    X      X
3    X  X
4 X         X
5        X     X

Ihned je třeba vidět, že tato relace je reflexivní.

Otázka kolik symetrických relací existuje nad n-prvkovou možinou se vlastně ptá na to, kolik existuje takových tabulek nxn symetrických podle hlavní diagonály. Více formálně:

Ptáme se, kolik existuje symetrických matic nxn nad tělesem 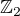v závislosti na n.

Pro každý prvek na úhlopříčce nebo nad ní máme dvě možnosti, ostatní prvky matice jsou už dané. Prvků na úhlopříčce je n, prvků pod ní je . Celkem máme 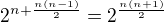možných symetrických relací.

Antisymetrické relace

Pro prvky nad úhlopříčkou můžeme volit ze dvou možností, prvky pod úhlopříčkou jimi jsou určeny. Prvky na úhlopříčce v relaci být nemohou. Možností je proto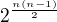

Reflexivní relace

Prvky na úhlopříčce v relaci být musí, pro 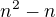ostatních prvků můžeme volit libovolně, proto 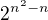reflexivních relací.

Ireflexivní relace

Prvky na úhlopříčce v relaci být nesmí, pro 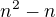ostatních prvků můžeme volit libovolně, proto 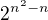relací.