Pravidelné spoření

Z MatWiki

Zadání

Kolik peněz bude mít v bance člověk po 10-ti letech, když tam na začátku každého roku vloží 2000 Kč? Roční úrok je 3 %. Zdanění úroků a bankovní poplatky neuvažujte.

Řešení

Vypíšeme si několik prvních let. Tak zjistíme pravidlo, podle kterého peníze v bance přibývají. Označíme:

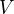$LaTeX: V$ pravidelný vklad

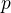$LaTeX: p$ roční úrok

Na začátku každého roku přibývá vklad, na koci roku přibývají úroky.

rok	začátek	konec
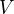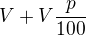1.	$LaTeX: V$	$LaTeX: V+V\frac p{100}$
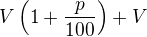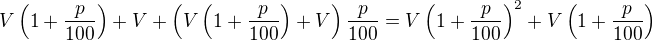2.	$LaTeX: V\left(1+\frac p{100}\right)+V$	$LaTeX: V\left(1+\frac p{100}\right)+V+\left(V\left(1+\frac p{100}\right)+V\right)\frac p{100}=V\left(1+\frac p{100}\right)^2+V\left(1+\frac p{100}\right)$
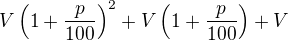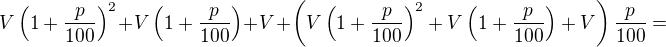3.	$LaTeX: V\left(1+\frac p{100}\right)^2+V\left(1+\frac p{100}\right)+V$	$LaTeX: V\left(1+\frac p{100}\right)^2+V\left(1+\frac p{100}\right)+V+\left(V\left(1+\frac p{100}\right)^2+V\left(1+\frac p{100}\right)+V\right)\frac p{100}=$
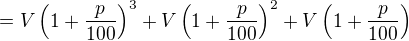		$LaTeX: =V\left(1+\frac p{100}\right)^3+V\left(1+\frac p{100}\right)^2+V\left(1+\frac p{100}\right)$

Pravidlo, podle kterého peníze přibývají, je zřejmé.

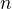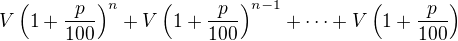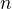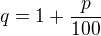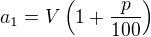Na konci $LaTeX: n$ -tého roku bude v bance $LaTeX: V\left(1+\frac p{100}\right)^n+V\left(1+\frac p{100}\right)^{n-1}+\dots+V\left(1+\frac p{100}\right)$ korun. Tento výraz ale představuje součet prvních $LaTeX: n$ členů geometrické posloupnosti s kvocientem $LaTeX: q=1+\frac p{100}$ a s prvním členem $LaTeX: a_1=V\left(1+\frac p{100}\right)$ .

Součet se tedy rovná

$LaTeX: S_n=a_1\frac{q^n-1}{q-1}=V\left(1+\frac p{100}\right)\frac{\left(1+\frac p{100}\right)^n-1}{\left(1+\frac p{100}\right)-1}=V\left(1+\frac p{100}\right)\frac{\left(1+\frac p{100}\right)^n-1}{\frac p{100}}$

Číselně pro zadané hodnoty: 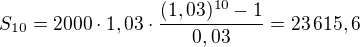$LaTeX: S_{10}=2000\cdot1,03\cdot\frac{(1,03)^{10}-1}{0,03}=23\,615,6$ .

Po deseti letech bude v bance 23 615,6 Kč.

Pravidelné spoření

Z MatWiki

Zadání

Řešení

Zobrazení

Osobní nástroje

Navigace

Hledat

Nástroje