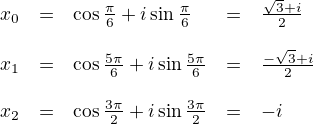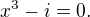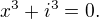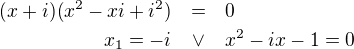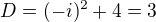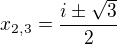Rovnice x^3=i
Z MatWiki
Obsah |
Zadání
V množině komplexních čísel řešte rovnici 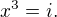
Řešení
Převedením na goniometrický tvar
Jednou z možností, jak řešit binomickou rovnici, je převedení pravé strany na goniometrický tvar.
Podle vztahu, který je uvedený zde, je
Dopočítáme jednotlivé kořeny a dostaneme
Rozkladem pomocí algebraických vzorců
Rovnici převedem na tvar
Nyní využijeme identity 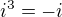 a dostaneme
a dostaneme
Dále použijeme vzorec 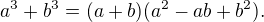
Rovnici 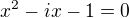 vyřešíme pomocí diskriminantu.
vyřešíme pomocí diskriminantu.
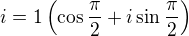
![LaTeX: x_k=\sqrt[3]{1}\left(\cos\frac{\frac\pi2+2k\pi}3+i\sin\frac{\frac\pi2+2k\pi}3\right)\quad k\in\{0,\ 1,\ 2\}](/math/307d0fa1fd38ed7b00fd15ce8583fc85.gif)