Rozklad polynomu čtvrtého stupně

Z MatWiki

Zadání:Rozložte na součin ireducibilních polynomů s reálnými koeficienty 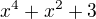$LaTeX: x^4+x^2+3$

Zdroj: Vlákno polynom na Matematickém fóru.

Řešení soustavou rovnic

Pro reálné x je hodnota polynomu vždy kladná, polynom nemá reálné kořeny a proto v rozkladu nebude žádný lineární polynom. Hledáme tedy koeficienty a, b, c,d, pro které 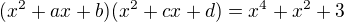$LaTeX: (x^2+ax+b)(x^2+cx+d)=x^4+x^2+3$ Porovnáním koeficientů

c+a=0 d+ac+b=1 ad+bc=0 bd=3

Z první rovnice c=-a, ze třetí pak a(b-d)=0. Nyní máme dvě možnosti:

a=0 vede na b+d=1, z poslední rovnice b(1-b)=3, což nemá reálné řešení. P
b-d=0 dá ze třetí rovnice 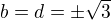$LaTeX: b=d=\pm\sqrt{3}$ , ze druhé rovnice pak 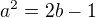$LaTeX: a^2=2b-1$ , možnost 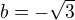$LaTeX: b=-\sqrt{3}$ lze vyloučit. Pro 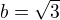$LaTeX: b=\sqrt3$ dokončíme rozklad

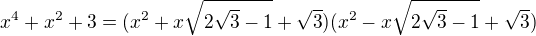
$LaTeX: x^{4}+x^{2}+3= (x^2 + x\sqrt{2\sqrt3 -1} + \sqrt3 )(x^2 -x\sqrt{2\sqrt3 -1}+ \sqrt3 )$

Řešení substitucí

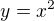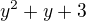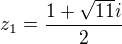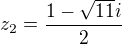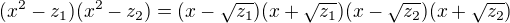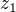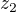Položíme $LaTeX: y=x^2$ , pak kořeny polynomu $LaTeX: y^2+y+3$ jsou $LaTeX: z_1=\frac{1+\sqrt{11}i}2$ , $LaTeX: z_2=\frac{1-\sqrt{11}i}2$ . V komplexním oboru lze zadaný polynom rozložit na $LaTeX: (x^2-z_1)(x^2-z_2)=(x-\sqrt{z_1})(x+\sqrt{z_1})(x-\sqrt{z_2})(x+\sqrt{z_2})$ . Protože jsou $LaTeX: z_1$ a $LaTeX: z_2$ čísla sdružená, jsou sdružené i jejich odmocniny a polynom lze psát jako 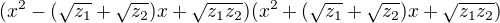$LaTeX: (x^2-(\sqrt{z_1}+\sqrt{z_2})x+\sqrt{z_1z_2})(x^2+(\sqrt{z_1}+\sqrt{z_2})x+\sqrt{z_1z_2})$ Z Vietových vztahů víme, že 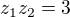$LaTeX: z_1z_2=3$ . Zbývá tedy vyčíslit 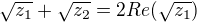$LaTeX: \sqrt{z_1}+\sqrt{z_2}=2Re(\sqrt{z_1})$ . K tomu lze použít soustavu rovnic. Dojdeme ke stejnému výsledku jako výše.

Rozklad polynomu čtvrtého stupně

Z MatWiki

Řešení soustavou rovnic

Řešení substitucí

Zobrazení

Osobní nástroje

Navigace

Hledat

Nástroje