Tečny ke kuželosečkám

Z MatWiki

Obsah

Pomocí přímky procházející tečnými body ("poláry")

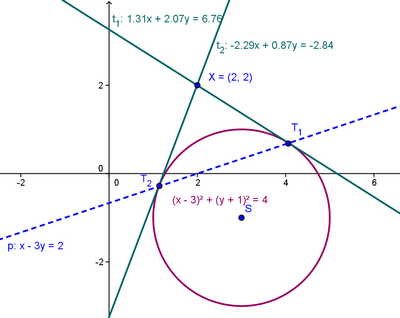
Kružnice

1) Kružnice ve tvaru 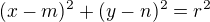$LaTeX: (x-m)^2+(y-n)^2=r^2$ a vnější bod $LaTeX: X[x_0;\,y_0]$ kde m; n jsou souřadnice středu kružnice

2) Pro poláru tj. přímku, která prochází tečnými body platí: 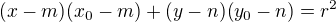$LaTeX: (x-m)(x_0-m)+(y-n)(y_0-n)=r^2$ .

3) Průsečíky poláry s kružnicí nám určí souřadnice tečných bodů T

4) Tečna je potom přímka procházející bodem X a bodem T (přímka určená dvěma body)

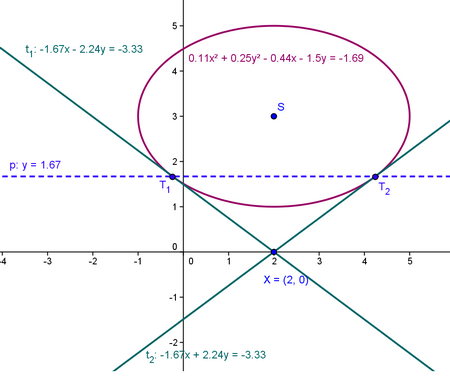
Elipsa

1) Elipsa ve tvaru 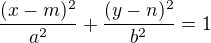$LaTeX: \frac{(x-m)^2}{a^2}+\frac{(y-n)^2}{b^2}=1$ a vnější bod $LaTeX: X[x_0;\,y_0]$ kde m; n jsou souřadnice středu elipsy

2) Pro poláru platí: 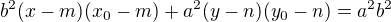$LaTeX: b^2(x-m)(x_0-m)+a^2(y-n)(y_0-n)=a^2b^2$

3) Průsečíky poláry s elipsou nám určí souřadnice tečných bodů T

4) Tečna je potom přímka procházející bodem X a bodem T (přímka určená dvěma body)

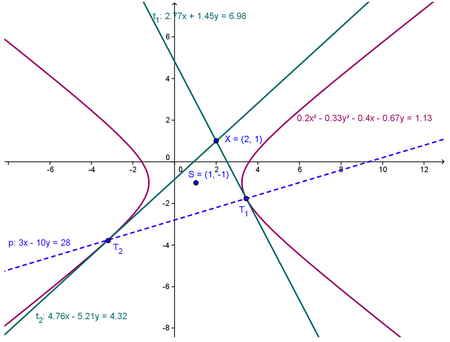
Hyperbola

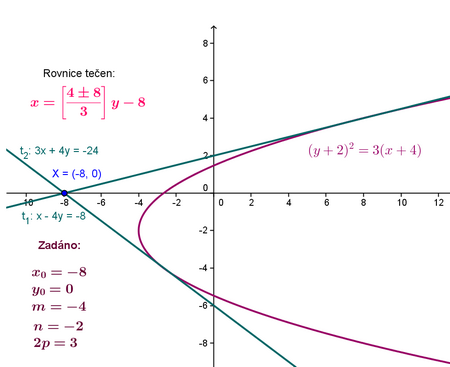
1) Hyperbola ve tvaru 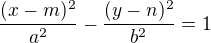$LaTeX: \frac{(x-m)^2}{a^2}-\frac{(y-n)^2}{b^2}=1$ a vnější bod $LaTeX: X[x_0;\,y_0]$ kde m; n jsou souřadnice středu hyperboly

2) Pro poláru platí: 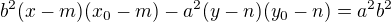$LaTeX: b^2(x-m)(x_0-m)-a^2(y-n)(y_0-n)=a^2b^2$

3) Průsečíky poláry s hyperbolou nám určí souřadnice tečných bodů T

4) Tečna je potom přímka procházející bodem X a bodem T (přímka určená dvěma body)

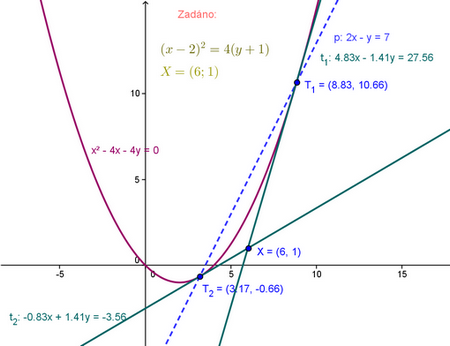
Parabola

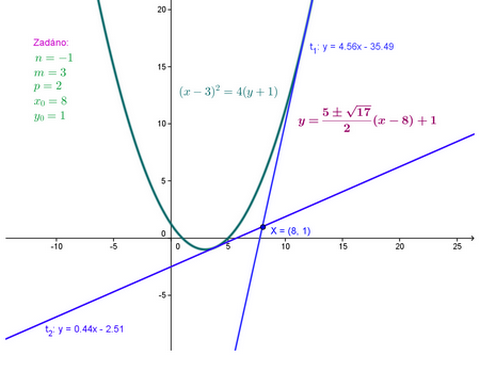
1) Parabola ve tvaru 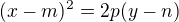$LaTeX: (x-m)^2=2p(y-n)$ a vnější bod $LaTeX: X[x_0;\,y_0]$ kde m; n jsou souřadnice vrcholu paraboly

2) Pro poláru platí: 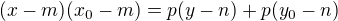$LaTeX: (x-m)(x_0-m)=p(y-n)+p(y_0-n)$

3) Průsečíky poláry s parabolou nám určí souřadnice tečných bodů T

4) Tečna je potom přímka procházející bodem X a bodem T (přímka určená dvěma body)

  Poznámka:  Pokud známe souřadnice tečného bodu kuželosečky, pak se rovnice tečny určí podle bodů 1) a 2) předchozího textu.

Pomocí tečny

Parabola

1) Parabola ve tvaru 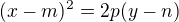$LaTeX: (x-m)^2=2p(y-n)$ a vnější bod $LaTeX: X[x_0;\,y_0]$ kde m; n jsou souřadnice vrcholu paraboly

2) Tečna má rovnici 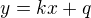$LaTeX: y=kx+q$

3) Po dosazení bodu 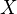$LaTeX: X$ je rovnice tečny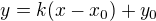 $LaTeX: y=k(x-x_0)+y_0$

4) Po dosazení 3) do 1) dostaneme kvadr. rovnici: 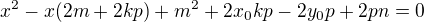$LaTeX: x^2-x(2m+2kp)+m^2+2x_0kp-2y_0p+2pn=0$

5) Protože je to tečna potom diskriminant 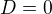$LaTeX: D=0$ a tedy: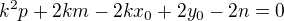 $LaTeX: k^2p+2km-2kx_0+2y_0-2n=0$

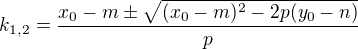
$LaTeX: k_{1,2}=\frac{x_0-m\pm\sqrt{(x_0-m)^2-2p(y_0-n)}}{p}$

6) Dosadíme do 3) a dostaneme rovnici tečny ve tvaru: 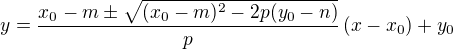$LaTeX: y=\frac{x_0-m\pm\sqrt{(x_0-m)^2-2p(y_0-n)}}{p}\left(x-x_0\right)+y_0$

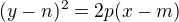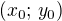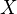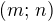7) Pro tečnu paraboly ve tvaru $LaTeX: (y-n)^2=2p(x-m)$ kde $LaTeX: (x_0;\,y_0)$ jsou souřadnice vnějšího bodu $LaTeX: X$ a $LaTeX: (m;\,n)$ souřadnice vrcholu platí vztah:

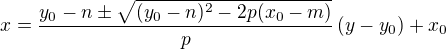
$LaTeX: x=\frac{y_0-n\pm\sqrt{(y_0-n)^2-2p(x_0-m)}}{p}\left(y-y_0\right)+x_0$

Kružnice

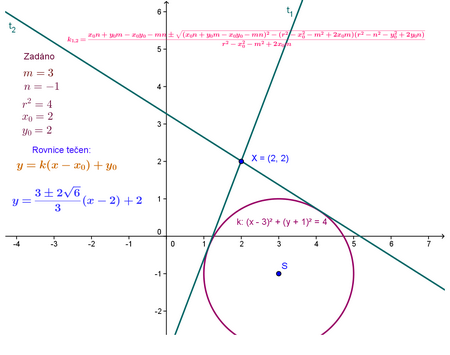
1) Kružnice ve tvaru 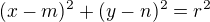$LaTeX: (x-m)^2+(y-n)^2=r^2$ a vnější bod $LaTeX: X[x_0;\,y_0]$ kde m; n jsou souřadnice středu kružnice

2) Tečna má rovnici 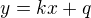$LaTeX: y=kx+q$

3) Po dosazení bodu 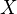$LaTeX: X$ je rovnice tečny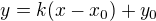 $LaTeX: y=k(x-x_0)+y_0$

4) Po dosazení 3) do 1) dostaneme kvadr. rovnici: 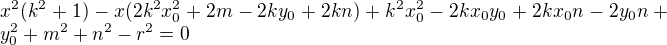$LaTeX: x^2(k^2+1)-x(2k^2x_0^2+2m-2ky_0+2kn)+k^2x_0^2-2kx_0y_0+2kx_0n-2y_0n+y_0^2+m^2+n^2-r^2=0$

5) Protože je to tečna potom 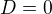$LaTeX: D=0$ a tedy:

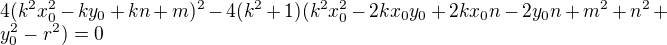
$LaTeX: 4(k^2x_0^2-ky_0+kn+m)^2-4(k^2+1)(k^2x_0^2-2kx_0y_0+2kx_0n-2y_0n+m^2+n^2+y_0^2-r^2)=0$

- úpravou dospějeme k rovnici:

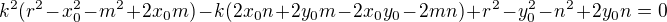$LaTeX: k^2(r^2-x_0^2-m^2+2x_0m)-k(2x_0n+2y_0m-2x_0y_0-2mn)+r^2-y_0^2-n^2+2y_0n=0$ a tedy:

$LaTeX: k_{1,2}=\frac{(x_0-m)(y_0-n)\pm\sqrt{\left[(x_0-m)(y_0-n)\right]^2-\left[(x_0-m)^2-r^2)(y_0-n)^2-r^2)\right]}}{(x_0-m)^2-r^2}$

6) Dosadíme do 3) a dostaneme rovnici tečny ve tvaru:

$LaTeX: y=\frac{(x_0-m)(y_0-n)\pm\sqrt{\left[(x_0-m)(y_0-n)\right]^2-\left[(x_0-m)^2-r^2)(y_0-n)^2-r^2)\right]}}{(x_0-m)^2-r^2}\left(x-x_0\right)+y_0$